문제 간략 설명: 철도 노선도에서 출발 정거장과 도착 정거장 사이를 최단 경로로 지나가는 모든 정거장의 이름을 알아내는 것이 이 게임의 목적입니다.
이 게임을 통해 여러분은 그래프 간선의 길이가 다를 경우에도 최단 경로를 찾을 수 있는 알고리즘을 학습합니다.
[사진]

[Rules_규칙]
목표:
TAN이 공개한 정보에는 각 정거장의 이름, 시간표, 운행 경로 등이 있습니다.
여러분은 지역 주민을 위해 대중교통 앱을 개발해야 합니다.
공개된 정보를 바탕으로 임의의 두 정거장 사이의 최단 경로를 구하는 것이 목표입니다.
규칙:
공개된 데이터에는 다음 정보가 문자열로 표현됩니다.
- 출발 정거장의 이름
- 모든 정거장의 정보
- 도착 정거장의 이름
- 각 정거장의 연결 정보
모든 정거장은 다음 정보를 가지고 있습니다. 한 줄에 한 정거장의 정보가 표시되며, 각 항목
은 콤마(,)로 구분합니다. 입력 순서는 다음 순서에 맞게 들어옵니다.
- 정거장의 고유 식별자
- 정거장의 이름(큰따옴표("")로 구분합니다)
- 정거장의 상세 설명(사용되지 않습니다)
- 정거장의 위도(각도)
- 정거장의 경도(각도)
- 구역의 고유 식별자(사용되지 않습니다)
- 정거장의 URL(사용되지 않습니다)
- 정거장의 종류
- 모정거장(사용되지 않습니다)

■ 각 정거장의 연결 정보
한 줄에는 두 정거장의 식별자가 공백으로 구분되어 표시됩니다.
이는 첫 번째 정거장에서 두 번째 정거장으로 이동할 수 있다는 뜻입니다.
각 정거장의 식별자는 StopArea 문구와 함께 입력됩니다.
정거장 간 이동은 한 방향으로만 가능합니다.
다시 말해, 두 정거장이 서로 이동 가능하려면 두 정거장의 연결 정보가 각각 표시되어야 합니다.
아래와 같은 경우는 LAIL과 GALH 정거장이 서로 이동 가능하게 됩니다.
| StopArea:LAIL -> StopArea:GALH | |
| StopArea:GALH -> StopArea:LAIL |
■ 정거장 사이의 거리
두 정거장 A와 B 사이의 거리는 다음 공식으로 계산합니다.
이 공식은 지구상의 두 지점 사이의 거리를 근사치로 계산하는 공식입니다.
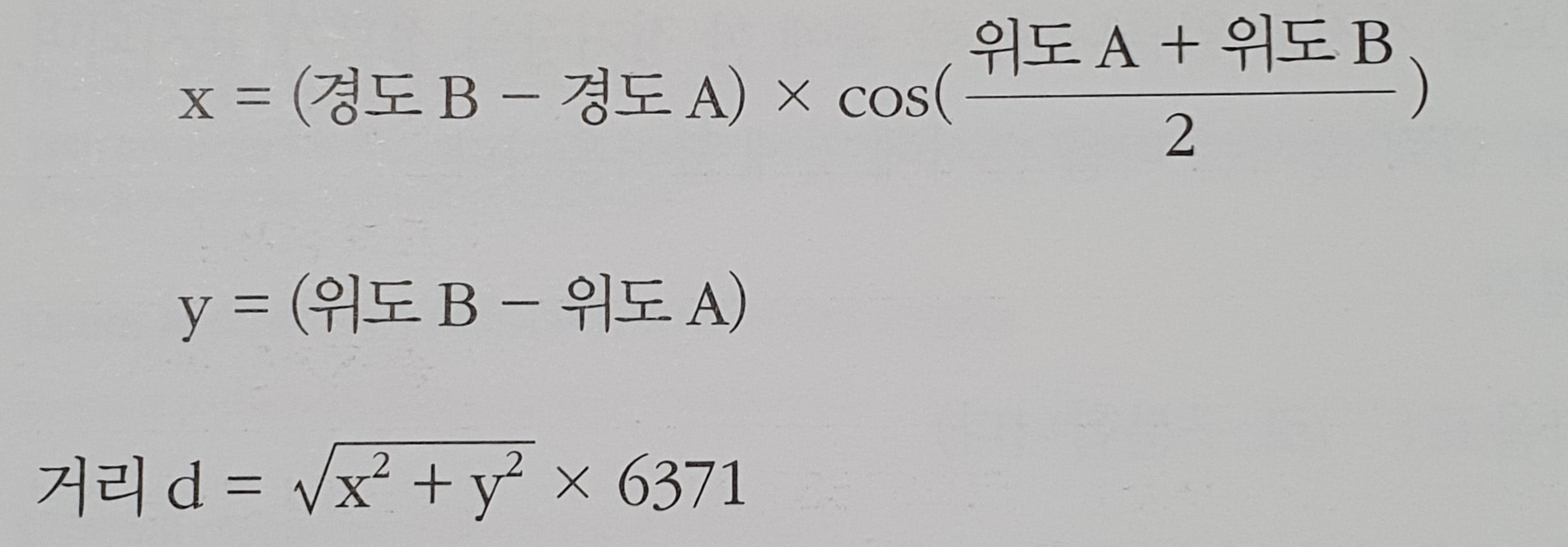
위 공식에서 6371은 지구의 반지름을 km로 환산한 수치입니다.
위도와 경도는 라디안(radian)으로 변환하여야 합니다.
■ Input_입력 받는 값
첫 번째 라인: 출발 정거장의 식별자
두 번째 라인: 도착 정거장의 식별자
세 번째 라인: 노선도에서 전체 정거장의 개수 N
다음 N라인: 각 정거장의 정보(모든 정거장의 정보가 입력됩니다)
다음 라인: 노선도에서 연결된 정거장 경로의 개수 M
다음 M라인: 연결된 두 정거장의 식별자
■ Output_출력해야 할 값
출발 정거장부터 도착 정거장까지 최단 경로로 지나가는 모든 정거장의 이름을 출력해야 합니다.
한 줄에 하나의 이름을 출력합니다.
최단 경로를 찾지 못할 경우 IMPOSSIBLE을출력합니다.
■Constraints_제약사항
0〈N〈10000
0〈M〈10000
[풀이 영상]
[문제]
https://www.codingame.com/training/hard/tan-network
Practice Pathfinding and Graphs with the exercise "TAN Network"
Want to practice Pathfinding and graphs? Try to solve the coding challenge "TAN Network".
www.codingame.com
[난이도]

[학습 개념]
[사전 지식]
아래 동영상과 블로그를 보고 다익스트라에 대한 개념을 공부하고 풀어보았습니다.
https://learning-e.tistory.com/41
[Algorithm] 다익스트라(Dijkstra) 알고리즘 with c#
근 몇 년 동안 이직을 2번이나 하느라,, 굉장히 바쁜 하루하루를 살았어요 그러다 보니 블로그를 거의 안 들어오게 되었고 정신 차려보니...23년5월.. 다시 정신을 부여잡고 내가 배우고 공부한 것
learning-e.tistory.com
아래 동영상을 보고는 최단 경로 알고리즘에 대해 더 구체적으로 알게 되었습니다.

http://qiao.github.io/PathFinding.js/visual/
PathFinding.js
qiao.github.io
위 링크는 아래 사진처럼 알고리즘이 적용된 길 찾기를 비주얼로 볼 수 있음
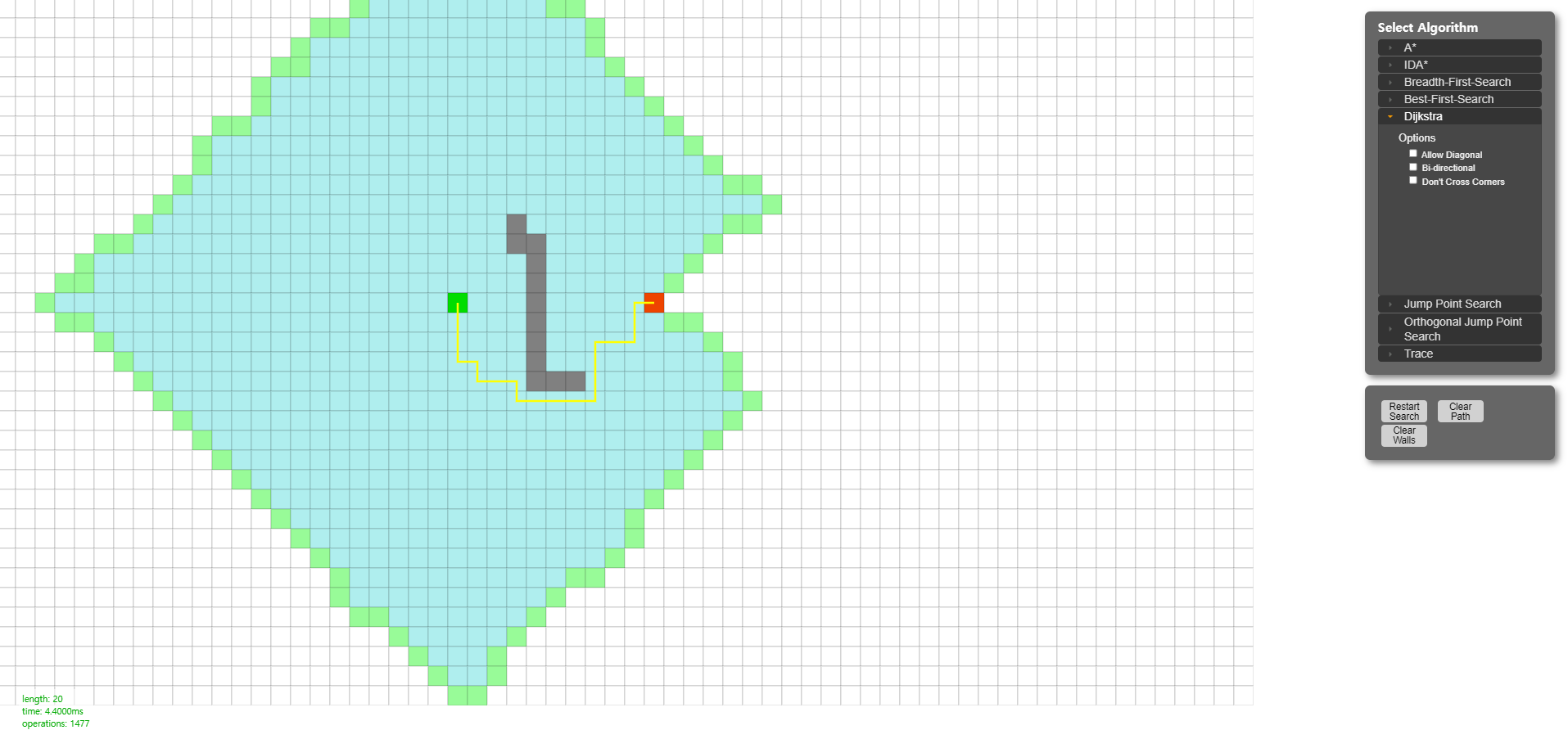
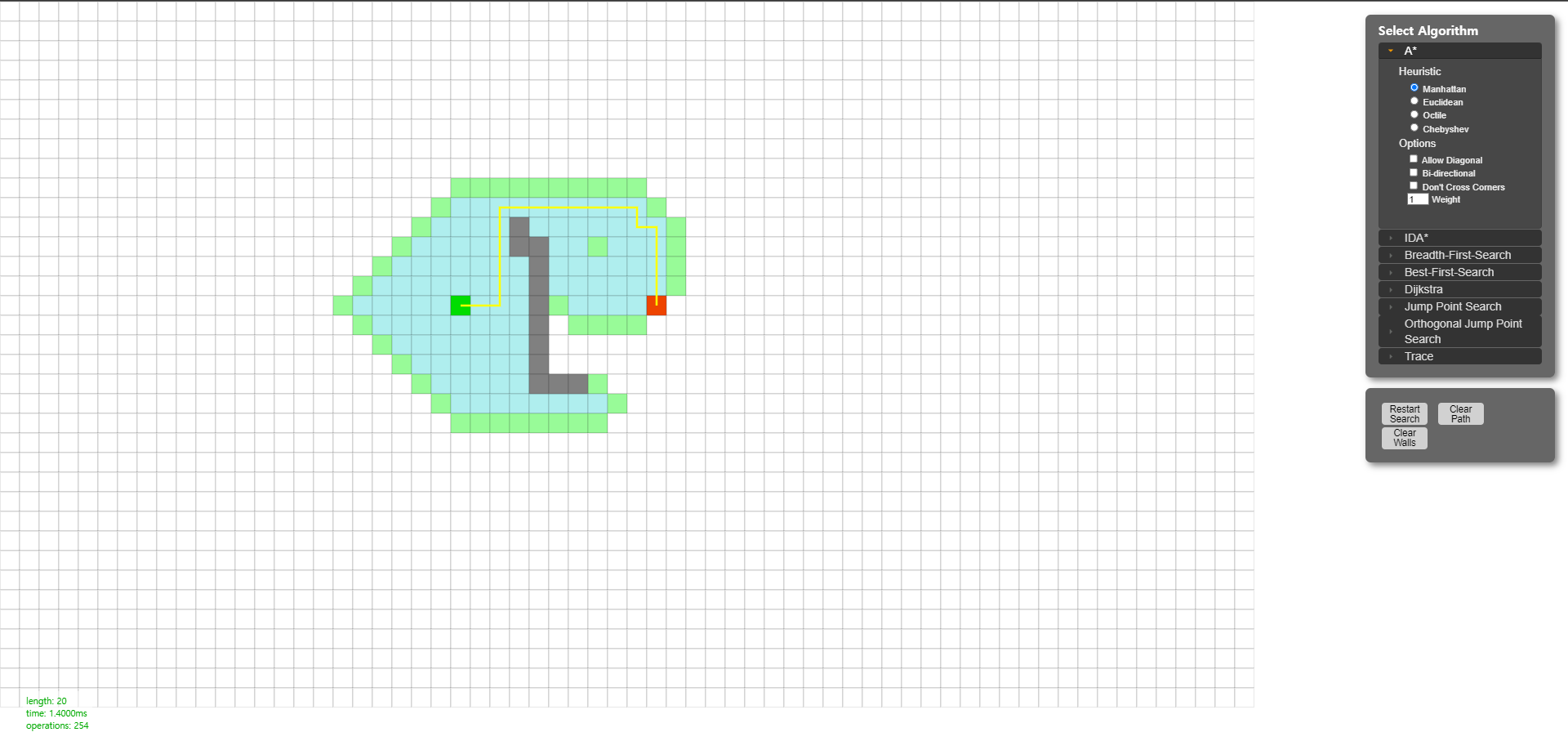
1. Dijkstra를 적용한 Version
[풀이 과정]
1. 입력 정보가 혼합된 문자열로 제공되기 때문에 먼저 정보들을 구분할 필요가 있었습니다.
2. 각 항목은 ','로 구분된 있으니 ', '를 기준으로 배열에 추가하고 정류장 이름은 "로 감싸져 있으니 "를 빈 문자열로 교체하는 과정을 통해 배열에 추가하였습니다.
3. 그 후 이 정보들을 담을 객체가 필요해졌으므로 NodeInformation 클래스를 통해 이 정보들을 담고 리스트로 정류장들의 정보를 관리해야겠다는 필요를 느껴 구현했습니다..
4. 간선 연결에 필요한 정보를 받을 때도 공백을 기준으로 정보가 나눠져 있으니 분리하여 배열에 담고,
문제에 나와있는 정거장 사이의 거리 함수를 구현해 간선의 가중치를 구현해 주었습니다.
5. 이제 간선을 연결해 주는 기능이 필요한데 이거는 사전지식에 있는 다익스트라 알고리즘 코드를 보며 아이디어를 얻어 다익스트라 클래스를 만들었습니다.
6. 인접 노드들은 딕셔너리 클래스로 구현하였습니다.
Key는 문자열 자료형으로 가중치가 있는 그래프를 구현하기 위해 Value는 ValueTuple를 자료형으로 하는 리스트를 만들어 인접 노드의 이름과 가중치를 같이 담았습니다.
7. 그리고 생성자, 노드를 추가하는 메소드, 간선을 추가하는 메소드를 만들었습니다.
노드 추가 메소드에는 정류장 식별자를 넘겨주고, 건선 추가 메소드에는 연결하는 두 개의 정류장 식별자와 간선의 가중치를 넘겨주었습니다.
8. 그리고 이제 다익스트라 알고리즘을 활용한 최단 경로 찾는 함수를 호출해 리스트를 반환받아
최단 경로가 없는 경우 IMPSSIBLE을 출력하고 아니라면 최단 경로의 정류장 이름을 출력하게 하였습니다.
9. 다익스트라 메소드는 다음과 같은 단계로 동작합니다.
- 노드들의 거리와 이전 노드들을 저장할 딕셔너리를 생성하였습니다.
- 거리를 기준으로 오름차순으로 정렬하는 우선 순위 큐를 생성합니다.
- 모든 노드의 가중치를 무한대로 초기화합니다.
- 모든 노드의 이전 노드를 빈 문자열로 초기화합니다.
- 시작 노드의 거리를 0으로 설정합니다.
- 시작 노드를 우선순위 큐에 추가합니다.
- 우선순위 큐에서 거리가 가장 작은 노드를 선택합니다.
- 선택한 노드를 우선순위 큐에서 제거합니다.
- 선택한 노드의 인접 노드들 중에서 거리가 가장 작은 노드를 찾습니다.
- 선택한 노드에서 인접 노드로 가는 거리를 계산합니다.
- 인접 노드의 거리가 더 작으면 인접 노드의 거리를 업데이트합니다.
- 인접 노드의 이전 노드를 현재 노드로 업데이트합니다.
- 인접 노드를 우선순위 큐에 추가합니다.
- 7번부터 13번까지의 과정을 반복합니다.
- 최단 경로를 저장할 리스트 만듭니다.
- 만약 도착 노드의 이전 노드가 없고 출발 노드와 도착 노드가 다르다면 빈 리스트를 반환합니다.
- 아니라면 리스트 시작 부분에 도착 노드부터 시작해서 이전 노드들을 추가합니다.
[소스 코드]
using System;
using System.Linq;
using System.Collections.Generic;
namespace Dijkstra
{
public class NodeInformation
{
public string ID; // 노드의 식별자
public string Name; // 노드의 이름
public double Latitude, Longitude; // 노드의 위도와 경도
public int StopType; // 정류장 유형
public List<NodeInformation> Neighbors { get; set; } // 인접한 노드들의 리스트
public NodeInformation(string ID_, string Name_, double Latitude_, double Longitude_, int StopType_)
{
ID = ID_;
Name = Name_;
Latitude = Latitude_;
Longitude = Longitude_;
StopType = StopType_;
}
}
public class Graph
{
int V; // 노드의 수
Dictionary<string, List<(string vertex, double distance)>> adjList; // 인접 리스트
public Graph(int vertices)
{
V = vertices;
adjList = new Dictionary<string, List<(string, double)>>();
}
public void AddNode(string value)
{
adjList.Add(value, new List<(string vertex, double distance)>());
}
public void AddEdge(string start, string end, double weight)
{
adjList[start].Add((end, weight));
}
public List<string> Dijkstra(string start, string end)
{
Dictionary<string, double> distance = new Dictionary<string, double>(); // 노드 n의 가중치를 저장하는 딕셔너리
Dictionary<string, string> previous = new Dictionary<string, string>(); // 최단 경로에서 각 노드의 이전 노드를 저장하는 딕셔너리
SortedSet<(string vertex, double distance)> priorityQueue = new SortedSet<(string vertex, double distance)>
(Comparer<(string vertex, double distance)>.Create((a, b) => a.distance.CompareTo(b.distance)));
foreach (var item in adjList)
{
distance[item.Key] = double.MaxValue; // 모든 노드의 거리를 무한대로 초기화
previous[item.Key] = string.Empty; // 모든 노드의 이전 노드를 빈 문자열로 초기화
}
distance[start] = 0.0; // 시작 노드의 거리를 0으로 설정
priorityQueue.Add((start, 0.0)); // 시작 노드를 우선순위 큐에 추가
while (priorityQueue.Count > 0)
{
(string current, double Dist) = priorityQueue.Min; // 우선순위 큐에서 거리가 가장 작은 노드를 선택
priorityQueue.Remove(priorityQueue.Min); // 선택된 노드를 우선순위 큐에서 제거
if (Dist > distance[current])
{
continue; // 선택된 노드의 거리가 이미 더 작은 값으로 업데이트된 경우 건너뜀
}
foreach ((string neighbor, double weight) in adjList[current]) // 선택된 노드의 인접 노드들
{
double newDist = distance[current] + weight; // 선택된 노드를 거쳐서 인접 노드로 가는 새로운 거리 계산
if (newDist < distance[neighbor]) // 새로운 거리가 더 작은 경우
{
distance[neighbor] = newDist; // 인접 노드의 거리 업데이트
previous[neighbor] = current; // 인접 노드의 이전 노드 업데이트
priorityQueue.Add((neighbor, newDist)); // 인접 노드를 우선순위 큐에 추가
}
}
}
List<string> shortestPath = new List<string>(); // 최단 경로를 저장할 리스트
if (previous[end] == string.Empty && !(start == end)) // 도착 노드에 이르는 경로가 없는 경우 (불가능한 경우)
{
shortestPath = new List<string>(); // 빈 리스트 반환
}
else
{
string current = end;
while (current != string.Empty)
{
shortestPath.Insert(0, current); // 최단 경로에 현재 노드 추가 (맨 앞에 삽입하여 역순으로 저장)
current = previous[current]; // 이전 노드로 이동
}
}
return shortestPath; // 최단 경로 반환
}
}
class Solution
{
static void Main(string[] args)
{
string startPoint = Console.ReadLine(); // 시작 지점 입력
string endPoint = Console.ReadLine(); // 도착 지점 입력
int N = int.Parse(Console.ReadLine()); // 정류장 수 입력
List<NodeInformation> Stops = new List<NodeInformation>(); // 정류장 리스트 생성
Graph graph = new Graph(N); // 그래프 객체 생성
for (int i = 0; i < N; i++)
{
string[] stopName = Console.ReadLine().Split(','); // 정류장 정보 입력 (쉼표로 구분된 값들)
string id = stopName[0]; // 정류장 식별자
double lat = double.Parse(stopName[3]); // 위도
double lon = double.Parse(stopName[4]); // 경도
string name = stopName[1].Replace("\"", string.Empty); // 정류장 이름 (따옴표 제거)
int stopType = int.Parse(stopName[7]); // 정류장 유형
graph.AddNode(id); // Astar 객체에 정류장 추가
Stops.Add(new NodeInformation(id, name, lat, lon, stopType)); // 정류장 리스트에 정류장 추가
}
int M = int.Parse(Console.ReadLine()); // 경로 수 입력
for (int i = 0; i < M; i++)
{
string[] route = Console.ReadLine().Split(' '); // 경로 정보 입력 (공백으로 구분된 값들)
double weight = CalcDist(Stops.Find(s => s.ID == route[0]), Stops.Find(s => s.ID == route[1])); // 경로의 가중치 계산
graph.AddEdge(route[0], route[1], weight);
}
List<string> shortestPath = graph.Dijkstra(startPoint, endPoint); // 최단 경로 탐색
if (shortestPath.Count <= 0) // 최단 경로가 없는 경우 (불가능한 경우)
{
Console.WriteLine("IMPOSSIBLE"); // "IMPOSSIBLE" 출력
}
else
{
foreach (var vertex in shortestPath) // 최단 경로 출력
{
string name = Stops.Find(s => s.ID == vertex)?.Name; // 노드 식별자에 해당하는 정류장 이름 가져오기
Console.WriteLine(name); // 정류장 이름 출력
}
}
}
static double CalcDist(NodeInformation node1, NodeInformation node2)
{
double x = (node2.Longitude - node1.Longitude) * Math.Cos((node1.Latitude + node2.Latitude) / 2); // 경도 차이 계산
double y = (node2.Latitude - node1.Latitude); // 위도 차이 계산
return DegToRad(Math.Sqrt(x * x + y * y) * 6371); // 거리 계산하여 반환
}
static double DegToRad(double degrees)
{
return (degrees * Math.PI / 180); // 도를 라디안으로 변환
}
}
}
[아쉬웠던 점]
다익스트라 알고리즘에 대한 개념을 이해하기에는 쉬었지만 코드를 나만의 힘으로 구현할 힘이 부족했던 점이 아쉬웠습니다.
결국 다른 사람의 코드들을 읽고 천천히 디버깅 하면서 결국은 알고리즘의 구동 방식을 이해하고 나만의 코드로 재탄생시켜 문제를 풀었지만 개념을 이해해 놓고 코드 구현에 자신감이 없어 머릿속이 하얘진 경험은 많이 아쉽고 더욱더 스스로 코드를 짜고 나만의 것으로 만드는 힘을 길러야겠다고 생각이 드는 문제였습니다.
하지만 점점 문제 풀이를 해나갈수록 이러한 힘이 커지고 있고 실력이 느는 게 눈에 보여 기쁩니다. ᕦ(ò_óˇ)ᕤ
[새롭게 알게 된 점]
1. 다익스트라 알고리즘에 대해 개념과 구동 과정을 이해하고 문제를 풀면서 이해도가 높아졌습니다.
2. Linq 메소드인 Find 메소드에 대해 알게 되어 써보았는데, Select 메소드와 컬렉션에서 특정 요소를 찾는 데 사용하는 건 비슷하지만 Find는 특정 요소를 찾고 해당 요소를 반환한다면, Select는 특정 조건을 만족하는 요소를 찾고 해당 요소를 반환한다는 차이점을 알게 되었습니다.
3. 다익스트라 알고리즘이 시작 노드를 기준으로 가장 가까운 노드부터 계속 탐색하기 때문에 원형으로 퍼져 나가는 경향이 있습니다. 그렇기 때문에 도착 노드가 출발 노드로부터 멀리 있는 경우 탐색 시간이 오래 걸리는 편입니다.
그리고 이런 문제를 개선한 A* 알고리즘에 대해 밑에 풀어보겠습니다.
2. A*를 적용한 Version
[풀이 과정]
1. 다익스트라 알고리즘 풀이와 코드는 거의 비슷합니다. 저는 새롭게 추가되고 수정된 부분을 집중적으로 소개하겠습니다.
A* 알고리즘은 다익스트라 알고리의 확장이라 할 수 있습니다.
2. 시작 노드부터 각 노드까지 최단 거리를 구하는 면에서는 동일하지만 다음 탐색할 노드를 정할 때는 시작 노드로부터의 최솟값뿐만 아니라, 각 노드에서 도착노드까지 예상거리를 같이 합산한 값이 최소가 되는 노드를 먼저 탐색합니다.
3. 아무래도 도착 노드에 가까운 노드를 먼저 탐색하기 때문에 다익스트라 알고리즘보다 빠른 시간에 목적지를 찾습니다.
4. 예상 거리는 보통 Heuristic(뜻: 직관적, 추측적을 의미하는 그리스어 단어) 근사 알고리즘을 사용합니다.
5. 저는 유클리드 거리 알고리즘을 써서 Heuristic 함수를 구현하였습니다.
유클리드 거리는 두 점 사이의 직선 거리를 계산하는 공식입니다.
6. 예를 들어, 서울의 위도는 37.56667°이고 경도는 126.97778°입니다.부산의 위도는 35.16667°이고 경도는 129.06667°입니다.서울과 부산 사이의 유클리드 거리는 약 392km입니다.지구의 지름을 고려하면, 서울과 부산 사이의 실제 거리는 약 389km입니다. 거의 비슷하죠?7. 그런 다음 다익스트라에서는 노드 n의 가중치로 모든 노드를 비교했다면, A*는 출발 노드로부터 노드 n까지의 경로 가중치 합 'G', 노드 n에서 도착 노드까지의 예상 거리의 합 'H', G + H인 'F'로 좀 더 효율적인 길찾기를 할 수 있습니다.
8. 그리고 A* 알고리즘에서는 Open List에서 가장 작은 비용을 가진 노드를 선택하여 검사하고, 해당 노드를 Closed List로 이동시킵니다. 그리고 해당 노드의 인접 노드들을 Open List에 추가합니다. 이 과정을 Open List가 비어있거나 도착 노드에 도달할 때까지 반복합니다.
9. Open List와 Closed List를 사용하는 이유는 다음과 같습니다:
Open List를 사용하여 현재까지 가장 작은 비용을 가진 노드를 선택하여 검사하므로, 빠르게 최적의 경로를 찾을 수 있습니다.
Closed List를 사용하여 이미 검사한 노드를 저장함으로써, 중복된 검사를 피하고 시간을 절약할 수 있습니다.
10. Open List와 Closed List를 사용하는 이유는 다음과 같습니다
- Open List를 사용하여 현재까지 가장 작은 비용을 가진 노드를 선택하여 검사하므로, 빠르게 최적의 경로를 찾을 수 있습니다.
- Closed List를 사용하여 이미 검사한 노드를 저장함으로써, 중복된 검사를 피하고 시간을 절약할 수 있습니다.
11. 이제 소개를 다 마쳤습니다. 소스 코드를 보면서 이해해도 충분히 이해하실거같습니다.
하지만, if (!openList.Any(x => x.vertex == neighbor) || newDist < G[neighbor]) 이 부분에 대한 소개만 더 자세히 하고 마무리 하겠습니다.
- 이웃 노드(neighbor)가 Open List에 포함되지 않은 경우: Open List에는 아직 방문하지 않은 노드들의 집합이 저장되어 있습니다. 만약 이웃 노드가 Open List에 포함되어 있지 않다면, 이웃 노드를 Open List에 추가하고 거리 정보(G)를 업데이트해야 합니다. 이는 최단 경로를 찾기 위해 이웃 노드를 검사해야 함을 의미합니다.
- 이웃 노드까지의 새로운 경로(newDist)가 현재까지 알려진 경로(G[neighbor])보다 짧은 경우: 이웃 노드에 대해 이미 알려진 경로(G[neighbor])보다 더 짧은 경로(newDist)를 찾았을 경우, 이웃 노드의 거리 정보(G)를 업데이트해야 합니다. 이는 현재까지 알려진 최단 경로보다 더 효율적인 경로를 찾았음을 의미합니다.
[소스 코드]
using System;
using System.Linq;
using System.Collections.Generic;
using static System.Formats.Asn1.AsnWriter;
namespace graph
{
public class NodeInformation
{
public string ID; // 노드의 식별자
public string Name; // 노드의 이름
public double Latitude, Longitude; // 노드의 위도와 경도
public int StopType; // 정류장 유형
public List<NodeInformation> Neighbors { get; set; } // 인접한 노드들의 리스트
public NodeInformation(string ID_, string Name_, double Latitude_, double Longitude_, int StopType_)
{
ID = ID_;
Name = Name_;
Latitude = Latitude_;
Longitude = Longitude_;
StopType = StopType_;
}
}
public class Graph
{
int V; // 노드의 수
Dictionary<string, List<(string vertex, double distance)>> adjList; // 인접 리스트
public Graph(int vertices)
{
V = vertices;
adjList = new Dictionary<string, List<(string, double)>>();
}
public void AddNode(string value)
{
adjList.Add(value, new List<(string vertex, double distance)>());
}
public void AddEdge(string start, string end, double weight)
{
adjList[start].Add((end, weight));
}
public List<string> Astar(string start, string end, List<NodeInformation> Stops)
{
double Heuristic(string cur, string end)
{
NodeInformation currentNode = Stops.Find(s => s.ID == cur); // 현재 노드
NodeInformation endNode = Stops.Find(s => s.ID == end); // 도착 노드
// 직선 거리(유클리드 거리)를 사용한 휴리스틱 계산
double dx = endNode.Latitude - currentNode.Latitude;
double dy = endNode.Longitude - currentNode.Longitude;
double approximateWeight = Math.Sqrt(dx * dx + dy * dy);
// 다른 노드와 이어져 있지 않다면 무한대를 반환
if (adjList[cur].Count <= 0)
{
return double.MaxValue;
}
return approximateWeight;
}
Dictionary<string, double> G = new Dictionary<string, double>(); // 출발 노드로부터 노드 n까지의 경로 가중치 합
Dictionary<string, double> H = new Dictionary<string, double>(); // 노드 n에서 도착 노드까지의 예상 거리의 합
Dictionary<string, double> F = new Dictionary<string, double>(); // F = G + H
Dictionary<string, string> previous = new Dictionary<string, string>(); // 최단 경로에서 각 노드의 이전 노드를 저장하는 딕셔너리
//Open List
SortedSet<(string vertex, double distance)> openList = new SortedSet<(string vertex, double distance)>
(Comparer<(string vertex, double distance)>.Create((a, b) => a.distance.CompareTo(b.distance)));
//Closed List
HashSet<string> closedList = new HashSet<string>();
//Dictionary init
foreach (var item in adjList)
{
G[item.Key] = double.MaxValue; // 모든 노드의 거리를 무한대로 초기화
H[item.Key] = Heuristic(item.Key, end); // 노드 n에서 도착 노드까지의 예상 거리를 초기화
previous[item.Key] = string.Empty; // 모든 노드의 이전 노드를 빈 문자열로 초기화
}
G[start] = 0.0; // 시작 노드의 거리를 0으로 설정
F[start] = G[start] + H[start];
openList.Add((start, F[start]));
while (openList.Count > 0)
{
(string current, double Dist) = openList.Min; // Open List의 최소 거리 노드
openList.Remove(openList.Min); // Open List에서 최소 거리 노드를 제거
if (current == end) // 도착 노드에 도달한 경우
break;
closedList.Add(current); // Closed List에 도착 노드를 추가
foreach ((string neighbor, double distance) in adjList[current]) // 현재 노드의 이웃 노드
{
if (closedList.Contains(neighbor)) // Closed List에 있는 노드는 건너뜀
continue;
double newDist = G[current] + distance; // 현재 노드에서 이웃 노드까지의 거리 계산
if (!openList.Any(x => x.vertex == neighbor) || newDist < G[neighbor]) // 이웃 노드가 Open List에 포함되지 않은 경우 or 현재 노드에서 이웃 노드까지의 거리가 G[neighbor]보다 작으면
{
G[neighbor] = newDist; // G[neighbor]를 현재 노드에서 이웃 노드까지의 거리로 갱신
F[neighbor] = G[neighbor] + H[neighbor];
openList.Add((neighbor, F[neighbor])); // 이웃 노드를 Open List에 추가
previous[neighbor] = current; // 이웃 노드의 이전 노드를 현재 노드로 갱신
}
}
}
List<string> shortestPath = new List<string>(); // 최단 경로를 저장할 리스트
if (previous[end] == string.Empty && !(start == end)) // 도착 노드에 이르는 경로가 없는 경우 (불가능한 경우)
{
shortestPath = new List<string>(); // 빈 리스트 반환
}
else
{
string current = end;
while (current != string.Empty)
{
shortestPath.Insert(0, current); // 최단 경로에 현재 노드 추가 (맨 앞에 삽입하여 역순으로 저장)
current = previous[current]; // 이전 노드로 이동
}
}
return shortestPath; // 최단 경로 반환
}
}
class Solution
{
static void Main(string[] args)
{
string startPoint = Console.ReadLine(); // 시작 지점 입력
string endPoint = Console.ReadLine(); // 도착 지점 입력
int N = int.Parse(Console.ReadLine()); // 정류장 수 입력
List<NodeInformation> Stops = new List<NodeInformation>(); // 정류장 리스트 생성
Graph graph = new Graph(N); // Astar 객체 생성
for (int i = 0; i < N; i++)
{
string[] stopName = Console.ReadLine().Split(','); // 정류장 정보 입력 (쉼표로 구분된 값들)
string id = stopName[0]; // 정류장 식별자
double lat = double.Parse(stopName[3]); // 위도
double lon = double.Parse(stopName[4]); // 경도
string name = stopName[1].Replace("\"", string.Empty); // 정류장 이름 (따옴표 제거)
int stopType = int.Parse(stopName[7]); // 정류장 유형
graph.AddNode(id); // Astar 객체에 정류장 추가
Stops.Add(new NodeInformation(id, name, lat, lon, stopType)); // 정류장 리스트에 정류장 추가
}
int M = int.Parse(Console.ReadLine()); // 경로 수 입력
for (int i = 0; i < M; i++)
{
string[] route = Console.ReadLine().Split(' '); // 경로 정보 입력 (공백으로 구분된 값들)
double weight = CalcDist(Stops.Find(s => s.ID == route[0]), Stops.Find(s => s.ID == route[1])); // 경로의 가중치
graph.AddEdge(route[0], route[1], weight);
}
List<string> shortestPath = graph.Astar(startPoint, endPoint, Stops); // 최단 경로 탐색
if (shortestPath.Count <= 0) // 최단 경로가 없는 경우 (불가능한 경우)
{
Console.WriteLine("IMPOSSIBLE"); // "IMPOSSIBLE" 출력
}
else
{
foreach (var vertex in shortestPath) // 최단 경로 출력
{
string name = Stops.Find(s => s.ID == vertex)?.Name; // 노드 식별자에 해당하는 정류장 이름 가져오기
Console.WriteLine(name); // 정류장 이름 출력
}
}
}
static double CalcDist(NodeInformation node1, NodeInformation node2)
{
double x = (node2.Longitude - node1.Longitude) * Math.Cos((node1.Latitude + node2.Latitude) / 2); // 경도 차이 계산
double y = (node2.Latitude - node1.Latitude); // 위도 차이 계산
return DegToRad(Math.Sqrt(x * x + y * y) * 6371); // 거리 계산하여 반환
}
static double DegToRad(double degrees)
{
return (degrees * Math.PI / 180); // 도를 라디안으로 변환
}
}
} [새롭게 알게 된 점]
1. A* 알고리즘에 대해 개념과 구동 과정을 이해하고 문제를 풀면서 이해도가 높아졌습니다.
2. opnelist와 closelist를 활용하면서 최단 경로 탐색 알고리즘을 효율적으로 개선하고 직관적으로 사용하는 법을 익혔습니다.
3. 휴리스틱 알고리즘에 대해 처음 알게 되었고, 유클리드 거리, 맨해튼 거리같은 두 점 사이를 구하는 방식이 이렇게 다양하다는 걸 알게 되었습니다..
실은 유클리드 거리 알고리즘을 못 믿고 내가 짠 코드는 time out으로 틀렸었습니다....
그러다가 풀이 6번에 적은 것처럼 거리 차이가 진짜 별로 안나는걸 보고 선조의 지혜를 느꼈습니다. (´・ω・`)!
//현재 노드에서 가중치가 최소인 이웃 노드로 이동하며, 이 과정을 반복하여 end까지의 대략적인 가중치를 계산
double Heuristic(string cur, string end)
{
double approximateWeight = 0.0;
string currentNode = cur;
while (currentNode != end && adjList[currentNode].Count > 0)
{
double maxWeight = double.MaxValue;
string nextNode = string.Empty;
foreach ((string neighbor, double distance) in adjList[currentNode])
{
if (distance < maxWeight)
{
maxWeight = distance;
nextNode = neighbor;
}
}
approximateWeight += maxWeight;
currentNode = nextNode;
}
//다른 노드와 이어져 있지 않다면 무한대를 반환
if (adjList[currentNode].Count <= 0)
{
return double.MaxValue;
}
return approximateWeight;
}'알고리즘 공부 > codingame 사이트 문제' 카테고리의 다른 글
| [Codingame] ROLLER COASTER(롤러코스터 대기열 시뮬레이션 - Circular queue, Dynamic programming (1) | 2023.06.12 |
|---|---|
| [Condingame] DEATH FIRST SEARCH - EPISODE 1(탈출 차단하기 - 그래프, 너비 우선 탐색) (0) | 2023.05.25 |
| [Condingame] SUPER COMPUTER(가장 효율적인 스케쥴-탐욕 알고리즘) (0) | 2023.05.11 |
| [Condingame] THE GIFT(돈을 나누는 가장 공평한 방식-탐욕 알고리즘) (0) | 2023.05.09 |
| [CodinGame] SHADOWS OF THE KNIGHT(이진 탐색으로 폭탄 찾기) (0) | 2023.05.08 |
![[Codingame] TAN NETWORK(거리별 최단 경로 찾기 - Dijkstra, A*)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fckh6Wy%2FbtsibpB00wa%2FKIaCfzTrtv8VKioQ6zCd81%2Fimg.png)